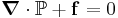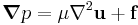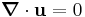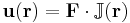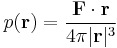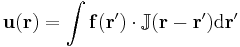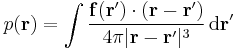Stokes flow
Stokes flow (named after George Gabriel Stokes), also named creeping flow, is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. 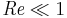 . This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature this type of flow occurs in the swimming of microorganisms and sperm[1] and the flow of lava. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally.
. This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature this type of flow occurs in the swimming of microorganisms and sperm[1] and the flow of lava. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally.
Contents |
Stokes equations
For this type of flow, the inertial forces are assumed to be negligible and the Navier–Stokes equations simplify to give the Stokes equations:
where 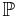 is the stress tensor, and
is the stress tensor, and 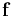 an applied body force. There is also an equation for conservation of mass. In the common case of an incompressible Newtonian fluid, the Stokes equations are:
an applied body force. There is also an equation for conservation of mass. In the common case of an incompressible Newtonian fluid, the Stokes equations are:
Here 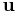 is the velocity of the fluid,
is the velocity of the fluid, 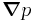 is the gradient of the pressure, and
is the gradient of the pressure, and  is the dynamic viscosity.
is the dynamic viscosity.
Properties
The Stokes equations represent a considerable simplification of the full Navier–Stokes equations, especially in the incompressible Newtonian case.[2][3] [4][5]
- Instantaneity
- A Stokes flow has no dependence on time other than through time-dependent boundary conditions. This means that, given the boundary conditions of a Stokes flow, the flow can be found without knowledge of the flow at any other time.
- Time-reversibility
- An immediate consequence of instantaneity, time-reversibility means then a time-reversed Stokes flow solves the same equations as the original Stokes flow. This property can sometimes be used (in conjunction with linearity and symmetry in the boundary conditions) to derive results about a flow without solving it fully. Time reversibility means that it is difficult to mix two fluids using creeping flow; a dramatic demonstration is possible of apparently mixing two fluids and then unmixing them by reversing the direction of the mixer.[6] [7]
While these properties are true for incompressible Newtonian Stokes flows, the non-linear and sometimes time-dependent nature of non-Newtonian fluids means that they do not hold in the more general case.
Methods of solution
1. By stream function
The equation for an incompressible Newtonian Stokes flow can be solved by the stream function method in planar or in 3-D axisymmetric cases
| Type of function | Geometry | Equation | Comments |
|---|---|---|---|
Stream function 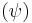 |
2-D planar | 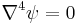 or or 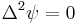 (biharmonic equation) (biharmonic equation) |
 is the Laplacian operator in two dimensions is the Laplacian operator in two dimensions |
Stokes stream function 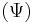 |
3-D spherical | 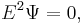 where where 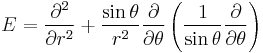 |
For derivation of the  operator see Stokes_stream_function#Vorticity operator see Stokes_stream_function#Vorticity |
Stokes stream function 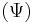 |
3-D cylindrical | 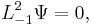 where where 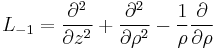 |
For 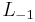 see [8] see [8] |
.
2. By Green's function
The linearity of the Stokes equations in the case of an incompressible Newtonian fluid means that a Green's function, 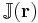 , for the equations can be found, where
, for the equations can be found, where 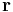 is the position vector. The solution for the pressure
is the position vector. The solution for the pressure  and velocity
and velocity 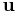 due to a point force
due to a point force 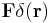 acting at the origin with
acting at the origin with 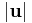 and
and  vanishing at infinity is given by[9]
vanishing at infinity is given by[9]
where
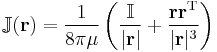 is a second-rank tensor (or more accurately tensor field) known as the Oseen tensor (after Carl Wilhelm Oseen).
is a second-rank tensor (or more accurately tensor field) known as the Oseen tensor (after Carl Wilhelm Oseen).
For a continuous-force distribution (density) 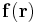 the solution (again vanishing at infinity) can then be constructed by superposition:
the solution (again vanishing at infinity) can then be constructed by superposition:
3. By Papkovich–Neuber solution
The Papkovich–Neuber solution represents the velocity and pressure fields of an incompressible Newtonian Stokes flow in terms of two harmonic potentials.
4. By boundary element method
Certain problems, such as the evolution of the shape of a bubble in a Stokes flow, are conducive to numerical solution by the boundary element method. This technique can be applied to both 2- and 3-dimensional flows.
See also
- Darcy's law
- Laminar flow
- Lubrication theory
- Hele-Shaw flow
- Oseen equations
- Poiseuille
- Slender-body theory
References
- ^ Dusenbery, David B. (2009). Living at Micro Scale. Harvard University Press, Cambridge, Mass. ISBN 978-0-674-03116-6.
- ^ Leal, L.G. (2007). Advanced Transport Phenomena:Fluid Mechanics and Convective Transport Processes.
- ^ Kirby, B.J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices.. Cambridge University Press. ISBN 978-0521119030. http://www.kirbyresearch.com/textbook.
- ^ Happel, J. & Brenner, H. (1981) Low Reynolds Number Hydrodynamics, Springer. ISBN 9001371159.
- ^ Batchelor, G. (2000). Introduction to Fluid Mechanics.
- ^ Dusenbery, David B. (2009). Living at Micro Scale, pp.46. Harvard University Press, Cambridge, Mass. ISBN 978-0-674-03116-6.
- ^ http://www.youtube.com/watch?v=p08_KlTKP50&feature=related
- ^ Payne, LE; WH Pell (1960). "The Stokes flow problem for a class of axially symmetric bodies". Journal of Fluid Mechanics 7 (04): 529–549. Bibcode 1960JFM.....7..529P. doi:10.1017/S002211206000027X.
- ^ Kim, S. & Karrila, S. J. (2005) Microhydrodynamics: Principles and Selected Applications, Dover. ISBN 0486442195.
- Ockendon, H. & Ockendon J. R. (1995) Viscous Flow, Cambridge University Press. ISBN 0521458811.